Case Study – Classification
Data classification is the method of determining a classifier or model that describes and discriminates several data classes from each other. Initially, the classification procedure applies some preprocessing tasks (data cleaning, data selection, data transformation etc.) to the original data. Then, the method divides the preprocessed data set into two different sections namely the training data set and the test data set. These data sets should be independent of each other to avoid biases. To ensure this, we use here k-fold cross-validation (CV) technique for distribution of the preprocessed dataset. We choose k=10 for this case study.
A classification technique creates a classification model which is alternatively known as a classifier. Classification basically consists of two different steps. The first step develops a i.e., classifier indicating a well-defined set of classes. Therefore, this is the training phase, where the classification technique constructs the model by learning from a given training dataset accompanied by their related class label attributes. After that, the classification model is suitable for prediction called the testing phase. This step evaluates the performance of the derived model using the test dataset based on the different performance measures for classification.
Several classification models are created in this case study for loan prediction problem. We take the preprocessed dataset (generated in the previous case study) for building our classifiers. The broad level stages of the classification procedure are shown below in Figure 1 for ease of understanding.
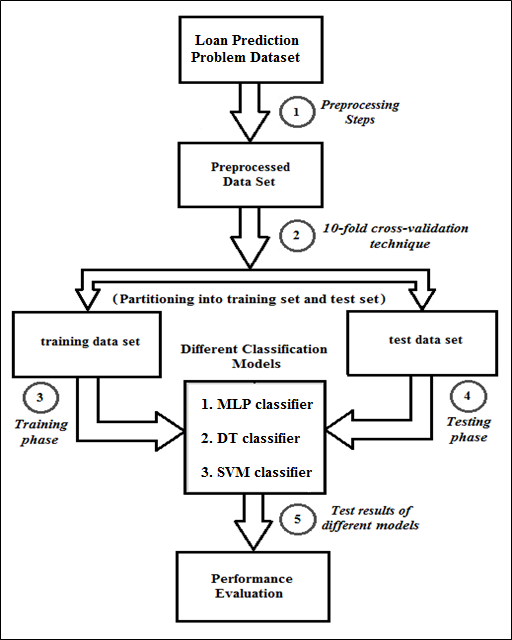
Figure 1: Broad level stages of the classification procedure
For classification task, we use here Python module (i.e. library) named scikit-learn which is denoted by sklearn in program. Built on NumPy, SciPy and Matplotlib, this library contains a lot of efficient tools for machine learning and statistical modeling including classification, regression, clustering and dimensionality reduction. The classifiers are implemented here one-by-one below using Python coding.
MLP (ANN) based classifier
The following code implements the MLP based classifier which is part of the ANN domain.
loan_mlp.py
# Step 1: Import libraries
import pandas as pd
import numpy as np
from sklearn.model_selection import KFold
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network import MLPClassifier
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.metrics import cohen_kappa_score
from sklearn.metrics import mean_squared_error
# Step 2: Load the dataset
df = pd.read_csv('loan.csv')
X = df.drop('Loan_Status', axis=1)
y = df['Loan_Status']
# Step 3: Split data into training and test sets using 10-fold CV
kf = KFold(n_splits=10, random_state=None, shuffle=True)
for train_index, test_index in kf.split(X):
X_train, X_test = X.iloc[train_index,:], X.iloc[test_index,:]
y_train, y_test = y.iloc[train_index], y.iloc[test_index]
# Step 4: To normalize our data
scaler = StandardScaler()
# Step 5: Fit only to the training data
scaler.fit(X_train)
# Step 6: Apply the transformations to the data
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
# Step 7: Training the model
mlp = MLPClassifier(hidden_layer_sizes=(5,12), max_iter=1000)
mlp.fit(X_train, y_train)
# Step 8: Predictions and Evaluation
predictions = mlp.predict(X_test)
accuracy = metrics.accuracy_score(predictions, y_test)
print("\nAccuracy: %s" % "{0:.2%}".format(accuracy)) # Print accuracy
print('\nConfusion Matrix:~ ')
print(confusion_matrix(y_test, predictions))
print('\nStatistical measures derived from confusion matrix:~ \n')
print(classification_report(y_test, predictions))
print('Kappa statistic value:~ ')
print(cohen_kappa_score(y_test, predictions))
print('\nRMSE:~ ')
print(np.sqrt(mean_squared_error(y_test, predictions)))
Output:
Accuracy: 83.61%
Confusion Matrix:~
[[ 8 7]
[ 3 43]]
Statistical measures derived from confusion matrix:~
precision recall f1-score support
0 0.73 0.53 0.62 15
1 0.86 0.93 0.90 46
avg/total 0.83 0.84 0.83 61
Kappa statistic value:~
0.5143312101910829
RMSE:~
0.40488816508945796
DT classifier
The program below implements the DT based classifier.
loan_dt.py
# Step 1: Import libraries
import pandas as pd
import numpy as np
from sklearn.model_selection import KFold
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.metrics import cohen_kappa_score
from sklearn.metrics import mean_squared_error
# Step 2: Load the dataset
df = pd.read_csv('loan.csv')
X = df.drop('Loan_Status', axis=1)
y = df['Loan_Status']
# Step 3: Split data into training and test sets using 10-fold CV
kf = KFold(n_splits=10, random_state=None, shuffle=True)
for train_index, test_index in kf.split(X):
X_train, X_test = X.iloc[train_index,:], X.iloc[test_index,:]
y_train, y_test = y.iloc[train_index], y.iloc[test_index]
# Step 4: Training the model
model = DecisionTreeClassifier()
model.fit(X_train, y_train)
# Step 5: Predictions and Evaluation
predictions = model.predict(X_test)
accuracy = metrics.accuracy_score(predictions, y_test)
print("\nAccuracy: %s" % "{0:.2%}".format(accuracy)) # Print accuracy
print('\nConfusion Matrix:~ ')
print(confusion_matrix(y_test, predictions))
print('\nStatistical measures derived from confusion matrix:~ \n')
print(classification_report(y_test, predictions))
print('Kappa statistic value:~ ')
print(cohen_kappa_score(y_test, predictions))
print('\nRMSE:~ ')
print(np.sqrt(mean_squared_error(y_test, predictions)))
Output:
Accuracy: 81.97%
Confusion Matrix:~
[[13 3]
[ 8 37]]
Statistical measures derived from confusion matrix:~
precision recall f1-score support
0 0.62 0.81 0.70 16
1 0.93 0.82 0.87 45
avg/total 0.84 0.82 0.83 61
Kappa statistic value:~
0.5766561514195583
RMSE:~
0.4246502900652006
SVM classifier
The following code implements the SVM based classifier.
loan_svm.py
# Step 1: Import libraries
import pandas as pd
import numpy as np
from sklearn.model_selection import KFold
from sklearn.preprocessing import StandardScaler
from sklearn import svm
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.metrics import cohen_kappa_score
from sklearn.metrics import mean_squared_error
# Step 2: Load the dataset
df = pd.read_csv('loan.csv')
X = df.drop('Loan_Status', axis=1)
y = df['Loan_Status']
# Step 3: Split data into training and test sets using 10-fold CV
kf = KFold(n_splits=10, random_state=None, shuffle=True)
for train_index, test_index in kf.split(X):
X_train, X_test = X.iloc[train_index,:], X.iloc[test_index,:]
y_train, y_test = y.iloc[train_index], y.iloc[test_index]
# Step 4: Normalize the data
scaler = StandardScaler()
# Step 5: Fit only to the training data
scaler.fit(X_train)
# Step 6: Now apply the transformations to the data
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
# Step 7: Training the model
model = svm.SVC(kernel='linear')
model.fit(X_train, y_train)
# Step 8: Predictions and Evaluation
predictions = model.predict(X_test)
accuracy = metrics.accuracy_score(predictions, y_test)
print("\nAccuracy: %s" % "{0:.2%}".format(accuracy)) # Print accuracy
print('\nConfusion Matrix:~ ')
print(confusion_matrix(y_test, predictions))
print('\nStatistical measures derived from confusion matrix:~ \n')
print(classification_report(y_test, predictions))
print('Kappa statistic value:~ ')
print(cohen_kappa_score(y_test, predictions))
print('\nRMSE:~ ')
print(np.sqrt(mean_squared_error(y_test, predictions)))
Output:
Accuracy: 88.52%
Confusion Matrix:~
[[14 6]
[ 1 40]]
Statistical measures derived from confusion matrix:~
precision recall f1-score support
0 0.93 0.70 0.80 20
1 0.87 0.98 0.92 41
avg/total 0.89 0.89 0.88 61
Kappa statistic value:~
0.7218241042345277
RMSE:~
0.3387537429470791
I hope that now you have got the confidence to deal with any type of classification problem in machine learning. In the next tutorial, I will discuss about some other classifiers which are worth mentioning.